用神经网络估计概率密度

机器学习算法通常估计未知数据生成过程的一阶矩（即均值）。然而，超越分布拟合一阶矩的应用在经济[2]、工程[3]和自然科学[4]等许多不同领域中都有应用。例如，一个观察金融市场并试图指导投资者的神经网络可能计算股票市场运动的概率，而不仅仅是运动的方向。为此，它可以使用概率密度函数来计算连续随机变量范围发生的总概率。

传统的密度估计方法（如此处）基于对函数的统计模型的初步选择，然后对其参数进行拟合。例如，一个输出均值（μ）和标准差（σ）参数的神经网络足以描述正态分布的密度函数：

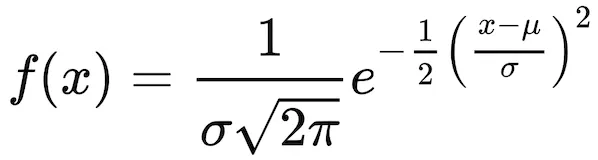
但是，如果事先不知道数据生成过程的先验知识呢？基于贝叶斯统计的一种替代方法最早由Aristidis Likas [1]提出。这种方法简单但有效，不需要对可用数据做出任何假设，而是从训练有素的神经网络输出中提取概率密度函数，该神经网络使用包括原始数据和一些已知分布的附加数据的数据库进行训练。不幸的是，原始实现不适合现代计算环境，因此在本文中，我将展示如何在Python和TensorFlow的背景下使用该方法。

1、设计数据生成过程

为了说明目的，我们可以创建一些简单的数据生成过程，如下所示，其中结果是使用单位指数X的条件正态分布生成的。因此，每个个体都将根据X具有其独特的概率密度函数（PDF）。

def hi_sample(N):  
    fx = lambda x: np.random.normal(loc = np.mean(x[:,0:-1],1), size=N)  
    X1 = np.random.exponential(1, size=N)  
    X2 = np.random.exponential(1, size=N)  
    Y =  fx(np.array([X1,X2]).T)  
    hi_data = [X1, X2, Y]  
    return np.array(hi_data).T  

train_array = hi_sample(5000)

生成的Y将具有以下分布：

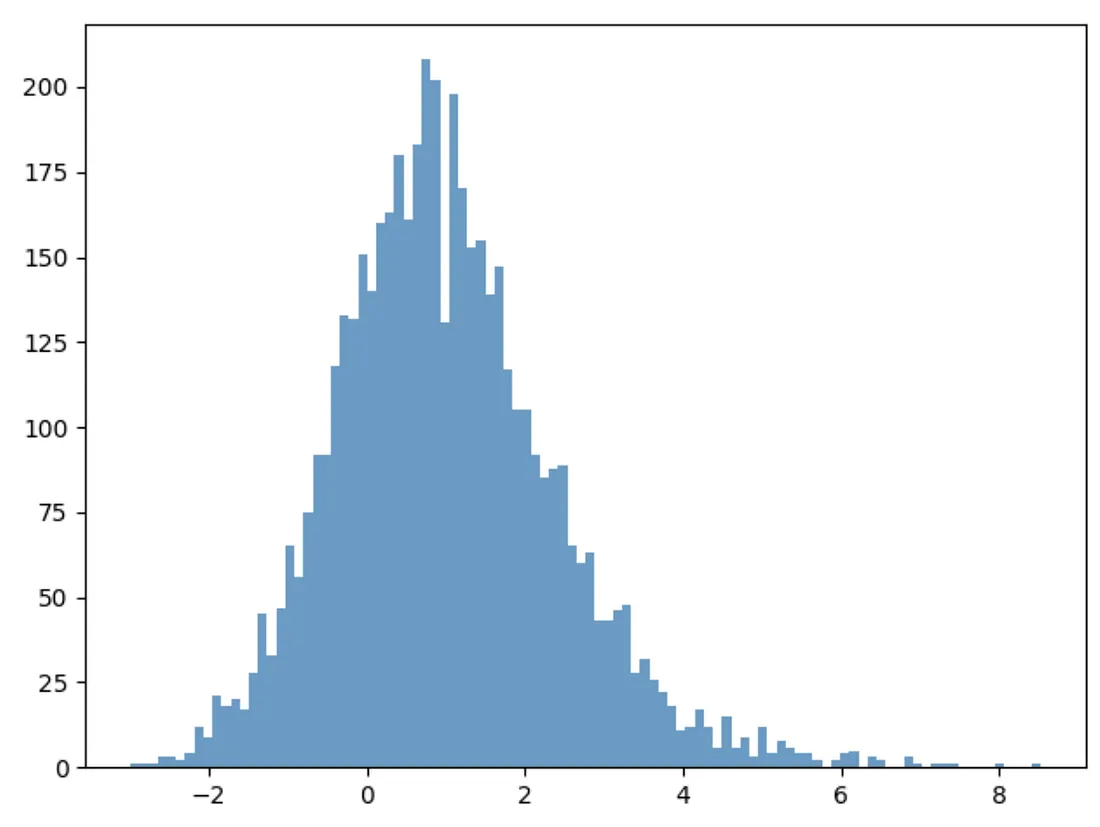
2、概率密度估计的基本方法

与其通过原始工作中的所有数学术语，这里我们重点介绍在Python中实现所需的基本步骤：

1) 用已知的数据生成过程（创建先验分布）扩充原始数据集，该过程来自参考PDF：P(ref)。在这里，我们假设扩充数据集中的所有个体的结果都来自标准正态分布：

train_array_0 = train_array.copy()  
train_array_0[:,-1] = metropolis_hastings_normal(train_array_0[:,-1]) #使用Metropolis-Hastings模拟器，用标准正态分布重新生成结果f(x)。   
train_data = [train_array,train_array_0]

2) 用二元分类神经网络拟合扩充数据集，该网络估计观察对X:=(x,f(x))是从pr(X)还是目标PDFp(X)生成的概率y(X)。它可能是一个简单的网络，如下所示：

def simple_nn(dim_x):  
    input_x = tfkl.Input(shape=(dim_x+1))  
    combined_layer = tfkl.Dense(dim_x)(input_x)  
    for i in range(5):  
        combined_layer = tfkl.Dense(dim_x)(combined_layer)  
        combined_layer = tfkl.Dropout(0.1)(combined_layer)  
    out = tfkl.Dense(1, activation='sigmoid')(combined_layer)  
    model = tf.keras.Model(inputs = input_x, outputs=out)  
    model.compile(loss = 'binary_crossentropy',  
                  optimizer=tf.keras.optimizers.RMSprop(lr=0.001))  
    return model

3) 使用贝叶斯理论计算目标概率密度函数：

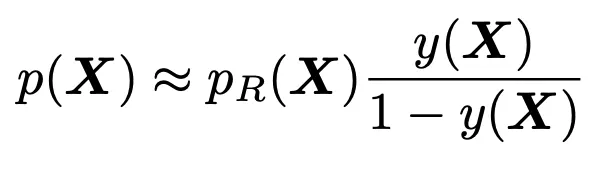
因此，使用专门增强的数据集训练NN会产生一个神经函数y(X)，从而可以推断出未知的PDFp(X)，使用中间任意PDFpr(X)：

conditional_y = pdf_function_i(x).numpy()  
reference_dense =  norm.pdf(x[:,-1]).reshape(-1, 1) #norm(loc = np.sum(x[:,0:-1],1)).pdf(x[:,-1]).reshape(-1, 1)  
conditional_dense = (conditional_y / np.clip(1 - conditional_y, a_min=1e-3, a_max=1.0))  * reference_dense

现在让我们绘制估计的PDF（conditional_dense）与真实PDF：

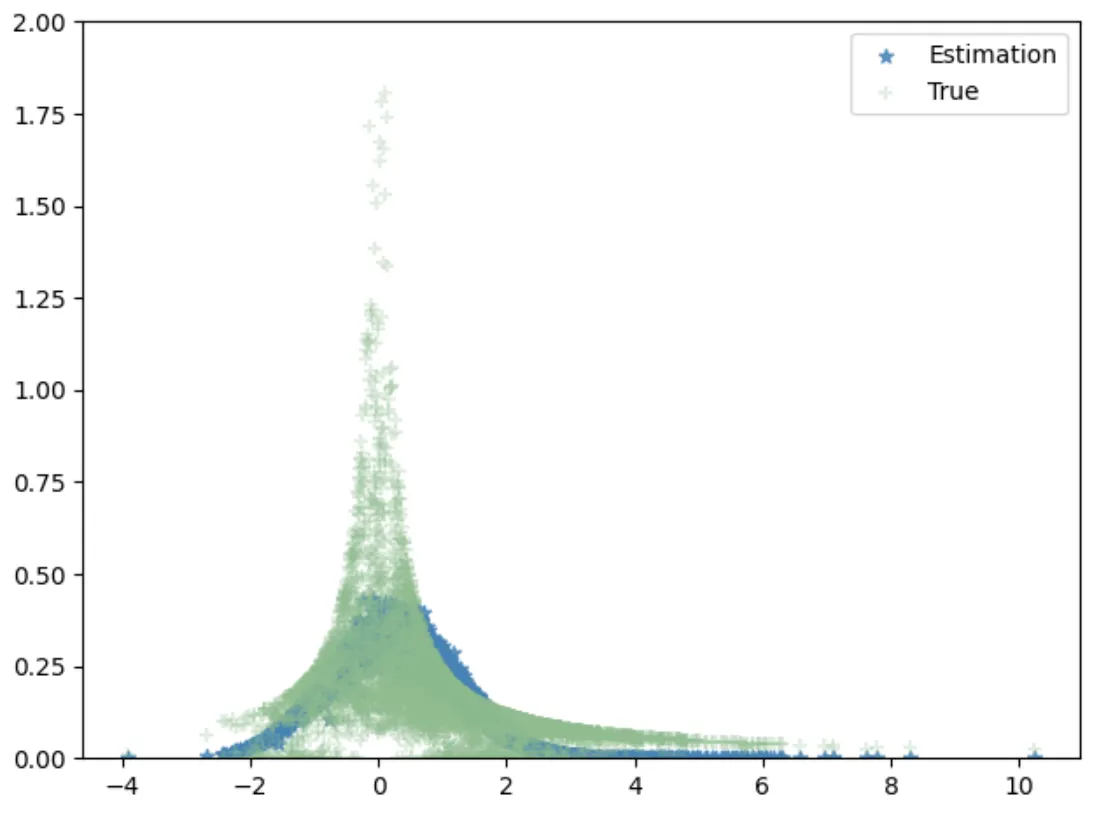
请注意，这里的每个个体点都具有给定X的正态分布。

让我们看看从标准密度函数派生的一些其他条件分布的估计：

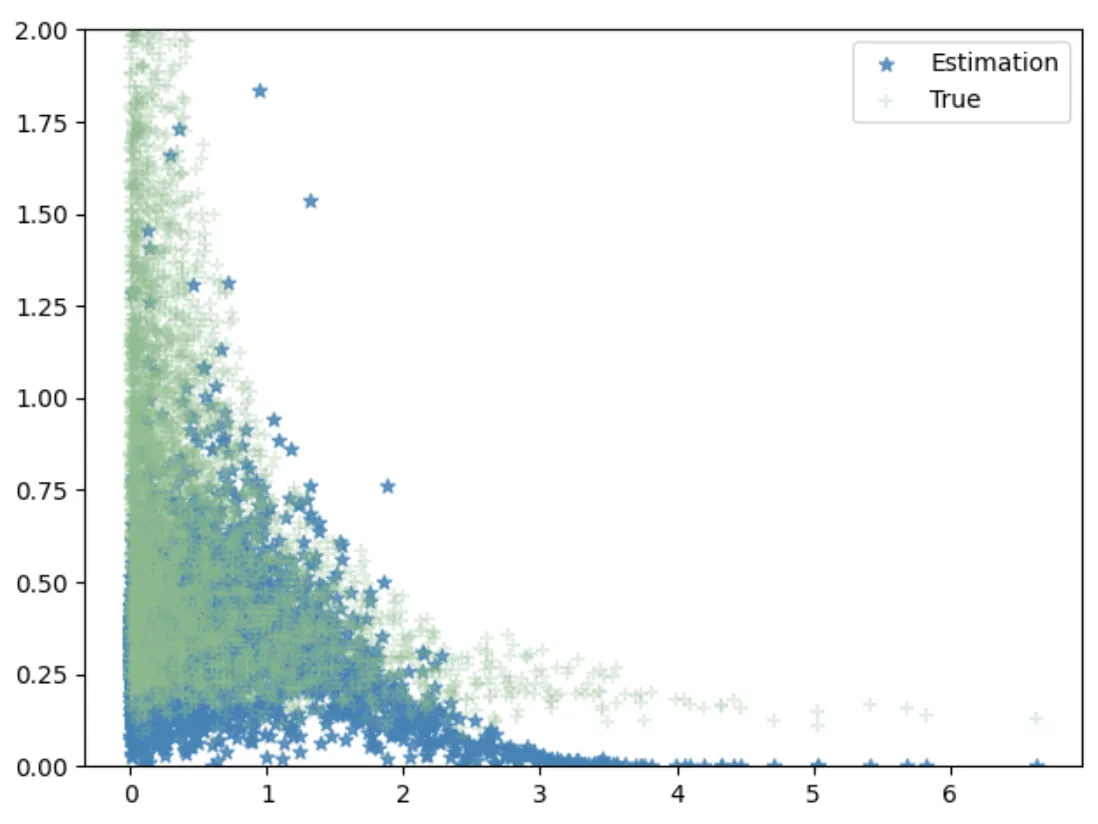
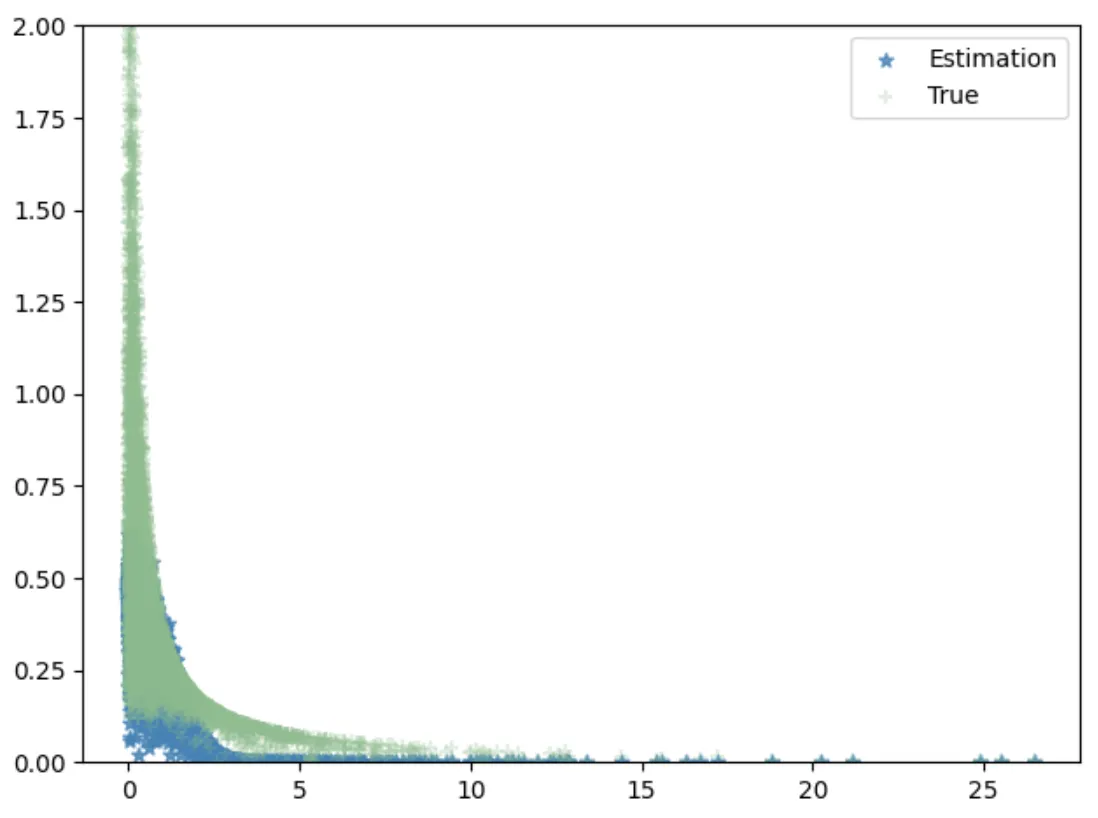
我们能够使用相同的标准正态先验，从不同的原始数据生成过程中获得相当准确的个体PDF估计。我们能否进一步改进估计？是的。在Leonardo Reyneri等人[5]的另一项工作中，作者建议使用初始估计的PDFp’(X)作为调整估计的先验。也就是说，我们重复步骤1到2，将标准正态先验替换为p’(X)，并在步骤三中估计以下数量：

因此，我们可以得到原始PDF估计的一次调整。这种直觉类似于自编码器，如果神经网络无法区分估计的PDF和先验PDF，则估计的PDF将是最佳的。

原文链接：Beyond Single Point Estimations using Neural Networks

汇智网翻译整理，转载请标明出处