从零构建流匹配模型

扩散模型无处不在。它们可以生成令人惊叹的图像、视频，甚至音乐。但它们非常慢。仅仅为了创建一张图片就需要数百次去噪步骤。

最近，我遇到了另一种生成建模方法：流匹配（Flow Matching）。这种方法通过求解常微分方程（ODE）来生成新数据，而不是通过反转扩散过程。

所以我从零开始构建了它——数学、模型、训练循环、速度场。这篇文章是对这一过程的精炼讲解：对流匹配的理论、代码和视觉直觉的动手探索。

我将讲解流匹配背后的数学原理，如何实现训练和采样管道，以及这种方法与扩散模型的根本区别。在本文的最后，你将拥有一个在PyTorch中的工作流匹配模型，并对生成模型如何超越噪声调度和分数有更清晰的认识。

图1。 使用流匹配进行图像生成。模型学习从高斯噪声到复杂数据分布的平滑轨迹。来源：流匹配用于生成建模 (arXiv:2210.02747)

1、为什么不直接使用扩散？

让我们从你可能听说过的流行生成模型开始：扩散模型，特别是DDPM（去噪扩散概率模型）。这些模型通过逐渐反转将干净图像转化为噪声的过程来生成图像。

你通过逐步向数据添加噪声直到它变成纯高斯噪声来训练模型——实际上看着图像被模糊成静态。然后模型学会了如何去噪这个静态，这就是我们所说的学习分数函数，这只是数据分布的梯度。所有这些都是说它学会了预测指向原始干净图像的方向。

但问题是：当你想生成一张新图像时，你必须从噪声开始，并以相反的方式经过同样的过程，逐步去噪每一个。分数函数必须插入到 随机微分方程（SDE）中，这是对噪声随时间反转的数学描述。因此，即使模型完全训练好了，采样也需要你通过许多去噪步骤来遵循这个SDE，这些步骤由分数引导。

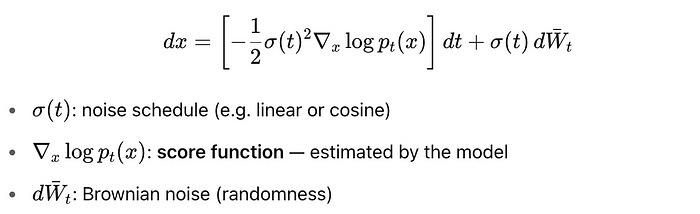
公式1。 在基于分数的扩散模型（如DDPM）中用于采样的随机反向过程。

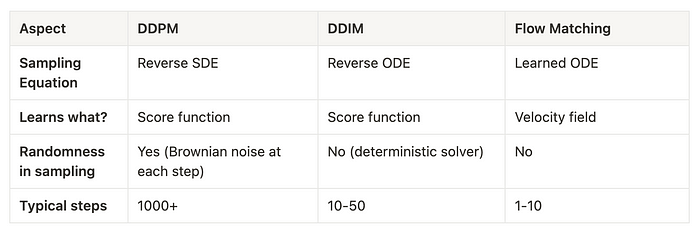
一些方法试图加快这个过程。例如，DDIM（去噪扩散隐式模型）是扩散的一个非随机版本，它消除了微分方程中的随机性。这些扩散ODE使用确定性求解器更快地反向运行。但即使这些模型仍然需要几十步去噪和几十次神经网络的前向传递。

公式2。 生成与SDE相同边缘分布的确定性反向过程，但不需要随机性。

如果我们跳过所有这些呢？如果我们不学习如何去噪，而是直接学习一个速度场，告诉我们如何将粒子从噪声推送到数据上的平滑路径？

这正是流匹配所做的——不是训练模型来反转噪声，而是训练它沿着连续路径移动样本到数据分布。

2、流匹配是如何工作的

为了生成图像，我们需要建模样本如何从一个简单的初始分布（比如高斯噪声）移动到一个复杂的分布（比如自然图像）。与基于去噪的方法不同，后者学习逐渐反转噪声，流匹配建模样本在两个分布之间的流动。

直觉提示

流匹配模型学习一条路径——一种连接噪声和数据的平滑、时间依赖的变换。这种解释使我们将图像生成视为一个运输问题。我们如何将一个点从起点移动到我们想要的位置？

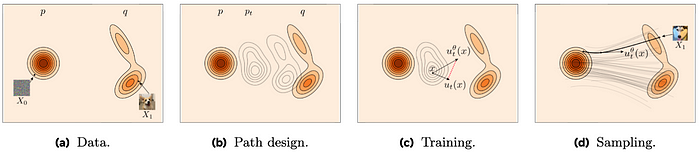
图2。 流匹配通过建模时间依赖的速度场来学习从噪声到数据的平滑路径。来源：改编自 Facebook AI Research Github

2.1 流匹配目标

我们从两个分布开始：

• p₀​: 一个简单的先验（例如标准高斯噪声）
• p₁: 复杂的最终分布（例如自然图像）

我们从每个分布中采样一个点，并用一条路径连接它们。最常见的方式是用一条直线连接它们：x(t) = (1 − t)x₀ + tx₁.

这被称为x₀和x₁之间的线性插值。（注意也可以使用其他插值方式（例如球面），但线性是最简单且在实践中效果很好——所以我们坚持使用这种方式。）

目标是学习一个时间依赖的速度场 f(x, t)，描述轨迹上每一点的速度。由于我们已经知道路径的地面真实速度，神经网络试图近似 x’(t) = x₁ − x₀.

所以，我们只需训练模型使其预测的速度与真实速度相匹配。

公式3。 流匹配的监督损失，比较从噪声到数据路径上的预测和真实速度。

2.2 使用流匹配进行采样

回想一下，网络学习了一个速度场 f(x, t)，将一个点从噪声移动到数据。在训练循环中，我们同时拥有 x₀ 和 x₁，但在生成时，我们只有 x₀。在采样时的目标是将一个噪声点推向 p₁ 分布，并达到看起来像自然图像的东西。

我们从一个样本 x₀ ~ p₀​（例如标准高斯噪声）开始。从那里我们定义一个从 t = 0 → 1 的时间网格，均匀分成一系列步骤。在每个时间步骤中，我们解决一个正向的ODE来更新样本：

公式4。 使用流匹配进行采样的更新规则。

向量场 f(x, t) 在每个步骤中使用当前的 x 和 t 来获取 x’(t) 的估计。一旦到达 t = 1，你将得到一个希望看起来像自然图像的样本。这个过程类似于跟随流场——我们“推动”样本沿着学习到的速度路径朝向数据。

3、实现讲解

在深入流匹配之前，我们需要一对要映射的分布。你可以从任何你想选择的噪声和数据分布开始，但为了我们的目的，我们选择两个简单的分布。

• p₀​: 二维标准高斯

def sample_source(batch_size):  
    # 从二维标准高斯（均值=0，标准差=1）中采样  
    return torch.randn(batch_size, 2)

• p₁: 二维棋盘数据集——由棋盘格网格中的高斯聚类组成的玩具数据集

def sample_target(batch_size):  
    # 在范围[-2, 2)中均匀采样x坐标  
    x1 = torch.rand(batch_size) * 4 - 2  

    # 采样y坐标：  
    # 步骤1：从[0, 1)中抽样  
    # 步骤2：随机减去0或2（通过torch.randint）  
    # 结果：值大致围绕-2或-1  
    x2_ = torch.rand(batch_size) - torch.randint(high=2, size=(batch_size, )) * 2  

    # 根据x1所在的bin是否为偶数添加垂直偏移  
    # 这会创建棋盘的交替行偏移  
    x2 = x2_ + (torch.floor(x1) % 2)  

    # 将x1和x2堆叠成（batch_size，2）向量，并缩放整个网格  
    data = 1.0 * torch.cat([x1[:, None], x2[:, None]], dim=1) / 0.45  

    return torch.tensor(data, dtype=torch.float32)

3.1 模型定义

我们构建一个小的神经网络来学习时间依赖的速度场 f(x, t)。由于我们的数据集并不太复杂，我们创建了一个小的MLP，输入为(x, t)，输出为与x相同维度的向量。

但由于t只是一个标量，我们首先使用两个全连接层将其映射到更高维空间。然后我们将这个时间嵌入与x连接，并通过几个带有SiLU激活的全连接层传递结果。

class FlowModel(nn.Module):  # 神经网络，用于学习时间依赖的速度场 f(x, t)  
  def __init__(self, input_dim=2, time_embed_dim=64):  
    super().__init__()  

    # 小型MLP，将时间标量t映射到更高维空间  
    self.time_embed = nn.Sequential(  
        nn.Linear(1, time_embed_dim),  
        nn.SiLU(),                     # 激活函数：Sigmoid线性单元  
        nn.Linear(time_embed_dim, time_embed_dim)  
    )  

    # 主网络，给定(x, 嵌入的t)预测速度  
    self.net = nn.Sequential(  
        nn.Linear(input_dim + time_embed_dim, 128),  # 输入：连接的x和t嵌入  
        nn.SiLU(),  
        nn.Linear(128, 128),  
        nn.SiLU(),  
        nn.Linear(128, 128),  
        nn.SiLU(),  
        nn.Linear(128, 128),  
        nn.SiLU(),  
        nn.Linear(128, 128),  
        nn.SiLU(),  
        nn.Linear(128, 128),  
        nn.SiLU(),  
        nn.Linear(128, input_dim)  # 输出：预测的速度（与x相同的维度）  
    )  

  def forward(self, x, t):  
    # 将时间t（形状：[batch_size, 1]）嵌入到更高维的向量  
    t_embed = self.time_embed(t)  

    # 沿最后一个维度连接位置x和时间嵌入  
    xt = torch.cat([x, t_embed], dim=-1)  

    # 通过网络预测(x, t)处的速度  
    return self.net(xt)

如第3.2节所述，目标是训练模型匹配路径上的真实速度。由于地面真实速度只是x₁ − x₀，我们可以通过最小化预测和真实速度之间的平方误差来强制这一约束。

def flow_matching_loss(model, x0, x1, t):  
  # 计算轨迹上每个t的插值点  
  xt = (1 - t) * x0 + t * x1  

  # 计算地面真实速度向量（轨迹上恒定）  
  v_target = x1 - x0  

  # 使用模型预测(x(t), t)处的速度  
  v_pred = model(xt, t)  

  # 计算每个样本预测和真实速度之间的平方误差  
  # 然后在整个批次上取平均  
  return ((v_pred - v_target) ** 2).mean()

3.2 训练

为了训练模型，我们从p₀和p₁中采样噪声和数据点。在每一步中，我们选择一个在[0, 1]范围内的随机时间，计算流匹配损失，并使用Adam更新参数。随着时间的推移，模型学习到连接两个分布的速度场。

num_steps = 10000  
batch_size = 512  
losses = []  

model = FlowModel().to(device)  
optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)  

for step in tqdm(range(num_steps)):  
  x0 = sample_source(batch_size).to(device)  
  x1 = sample_target(batch_size).to(device)  
  t = torch.rand(batch_size, 1).to(device)  # 随机插值时间 ∈ [0, 1]  

  loss = flow_matching_loss(model, x0, x1, t)  

  optimizer.zero_grad()  
  loss.backward()  
  optimizer.step()  

  losses.append(loss.item())  

  if step % 100 == 0:  
    print(f"Step {step} | Loss: {loss.item():.4f}")

3.3 采样

为了从我们训练好的模型中生成新的样本，我们从噪声分布中的一个点开始，并使用学习到的速度场f(x, t)将其向前推进。这是通过从t = 0到t = 1求解ODE来完成的，就像我们在第3.3节中描述的一样。我们使用scipy.integrate.solve_ivp，一个标准的ODE求解器，来数值积分学习到的速度场并产生位于目标分布中的输出。

def sample_flow(model, x0, t_span=(0, 1)):  
    """  
    通过学习的流演化x0以生成p1的样本。  
    """  
    def ode_func(t, x):  
        # 将输入x和时间t转换为适当的torch张量  
        x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(0).to(device)  
        t_tensor = torch.tensor([[t]], dtype=torch.float32).to(device)  

        # 不跟踪梯度预测速度  
        with torch.no_grad():  
            v = model(x_tensor, t_tensor)  

        # 返回速度作为NumPy数组（形状：[2]）  
        return v.squeeze(0).cpu().numpy()  

    # 使用学习到的速度场从t=0到t=1求解ODE  
    sol = solve_ivp(ode_func, t_span, x0.cpu().numpy(), t_eval=[t_span[1]])  

    # 返回t=1的最终状态（即预测的x1）  
    return sol.y[:, -1]

4、结果与可视化

我们为流匹配定义了一个简单的合成玩具问题，其中p₀​是一个二维高斯分布，而p₁是一个棋盘图案。这种设置允许我们轻松可视化学习到的流和中间诊断。

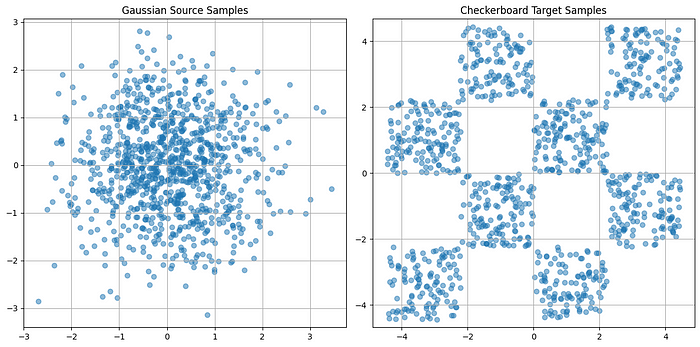
图3。 从二维标准高斯分布（左）和合成棋盘分布（右）中抽取的源样本。

4.1 训练损失曲线

损失在早期迭代中迅速下降，然后开始振荡。

图4。 10,000次优化步骤的训练损失曲线。

4.2 学习到的速度场

向量场随时间平滑演变。在t = 0时，流从中心向外，反映了向高斯分布的运动。在后期t时，流开始表现出更像棋盘的结构。

图5。 在各种时间t∈{0.0,0.25,0.5,0.75,1.0}时学习到的速度场快照

4.3 生成样本与目标样本

为了生成新的样本，我们使用scipy.integrate.solve_ivp从t = 0到t = 1集成学习到的速度场。定性地说，生成的样本与目标棋盘的形状和结构非常接近。

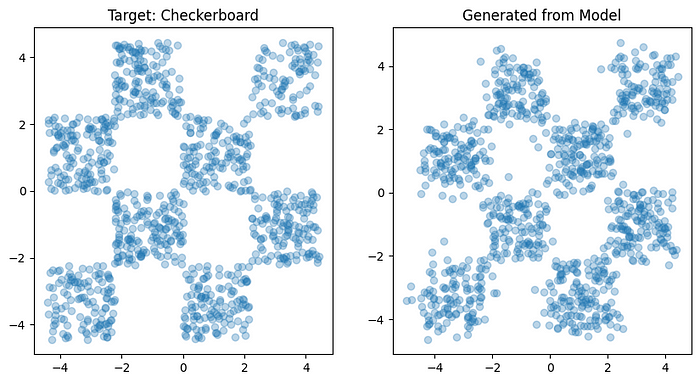
图6。 棋盘目标分布的真实样本（左）和通过集成学习流生成的样本（右）

5、局限性和扩展

虽然流匹配是分数匹配的一种简单而优雅的替代方案，但它确实面临一些限制。

• 没有采样保证
  流匹配绕过了对数似然，而是拟合了一个模型到速度场。虽然这种方法简化了训练，但它不再保证我们的生成样本在目标分布中。
• 推理时的集成成本
  要使用这种方法生成新样本，需要在推理时为每个输入样本求解ODE。这相比前馈模型或具有较少步骤的扩散采样来说计算成本较高。
• 需要速度监督
  流匹配需要访问地面真实速度。虽然这对于简单的合成数据集来说很容易，但对于现实世界的数据来说却变得极其困难。

为了解决这些限制，研究人员开发了几种改进方法。

• 结合分数模型的流匹配
  一些方法已经开始结合这两种模型——使用基于分数的目标来训练流匹配模型。这结合了两者的优点。
• 神经ODE求解器
  更先进的ODE求解器或甚至神经近似器可以通过学习流场中的高效解决方案来减少推理时间，从而在推理时实现更快的采样。

6、GitHub + Colab

查看 GitHub 仓库。

包含一个整洁的文件夹结构，包括：

• checkerboard_flow_matching.ipynb 笔记本
• images/ 文件夹用于可视化
• requirements.txt 用于轻松安装

安装：

git clone https://github.com/vickiiimu/checkerboard-FM-tutorial.git  
cd flow_matching  
pip install -r requirements.txt

在 Colab 中打开。读者可以直接在浏览器中fork并运行笔记本。

6、结束语

祝贺你——你刚刚从零开始构建了流匹配！

在过程中，我们介绍了流匹配的核心思想，探讨了它与传统扩散模型的不同之处，并重新实现了核心组件，如玩具2D数据集、向量场估计和ODE积分。如果你按照讲解操作，你现在拥有了一个你完全理解的流匹配模型。

无论你是来这里学习内部机制、原型化自己的想法，还是仅仅出于好奇心——这是你的沙盒。

原文链接：From Noise to Structure: Building a Flow Matching Model from Scratch

汇智网翻译整理，转载请标明出处