用 RAPIDS cuML 挖 Alpha 信号
RAPIDS cuML 加速器对于金融市场分析意义重大,因为处理股票收益率等大型数据集的scikit-learn代码在 CPU 上可能需要数小时,而利用 GPU 可以将计算时间缩短至数秒。

在 GTC 2025 大会上,NVIDIA 宣布 RAPIDS cuML 现在为 scikit-learn 提供 GPU 加速。cuML 加速器无需任何代码更改即可实现高达 50 倍的显著速度提升。这对于金融市场分析意义重大,因为处理股票收益率等大型数据集在 CPU 上可能需要数小时,而利用 GPU 可以将计算时间缩短至数秒。
在本指南中,您将对标普 500 指数股票的历史收益率进行主成分分析 (PCA)。然后,使用 PCA 来提取潜在的 alpha 信号。使用 RAPIDS,速度可提升 50 倍。即使在 CPU 上,运行速度也很快。设置:在配备 NVIDIA GPU 的机器上通过 conda 安装 RAPIDS。
1、什么是 PCA?为什么是 alpha?
PCA(主成分分析)提取投资组合收益的统计驱动因素。这些驱动因素被称为“alpha 因子”(或简称因子),因为它们产生的收益无法用市场指数等基准来解释。
量化交易员在交易策略中使用因子:提取成分,然后买入对某个有前景的因子敞口高的股票,卖出敞口低的股票。今天,您将使用 Python 入门级代码,通过复制粘贴的方式完成这项工作。
2、导入和设置
首先导入库。sklearn 用于构建统计模型;我们通过 Jupyter Notebook 加载 cuML 扩展以实现 GPU 加速。
%load_ext cuml.accel # Accelerates sklearn on GPU (RAPIDS magic!)
%matplotlib inline # Ensures plots display in notebook
import yfinance as yf
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # For 3D plotting
import requests # For fetching latest S&P 500 list from wikipedia
from io import StringIO接下来,从维基百科下载标普 500 指数代码,并通过 yfinance 获取收益率。
# Download latest S&P 500 symbols from Wikipedia
# Set a User-Agent to avoid 403 Error
headers = {
'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/91.0.4472.124 Safari/537.36'
}
# Try fetching S&P 500 symbols from Wikipedia
url = "https://en.wikipedia.org/wiki/List_of_S%26P_500_companies"
try:
response = requests.get(url, headers=headers)
response.raise_for_status() # Check for HTTP errors
tables = pd.read_html(StringIO(response.text))
print(f"Found {len(tables)} tables.")
main_table = tables[0] # First table is S&P 500 constituents
print("Main table columns:", main_table.columns.tolist())
print("First few symbols:", main_table['Symbol'].head().tolist())
snp_symbols = main_table['Symbol'].tolist()
except Exception as e:
# alternatively you can load from a csv or even list manually if everything fails
print(f"Error fetching data from Wikipedia: {e}")
# Fallback: Use a local CSV or alternative source
print("Using fallback: Provide a local CSV or alternative source.")
# Example: Save symbols manually or load from a file
# snp_symbols = ['AAPL', 'MSFT', 'GOOGL', ...] # Replace with actual list or CSV
# For now, raise error to prompt user action
raise SystemExit("Please provide a local CSV with S&P 500 symbols or fix the network issue.")
# Clean symbols for yfinance
symbols = [sym.replace(".", "-") for sym in snp_symbols] # e.g., BRK.B -> BRK-B获取标普 500 指数后,您可以使用 yfinance 轻松下载数据。
# Test validity for yfinance data
data = yf.download(symbols, start="2020-01-01", end="2025-10-15")
if data.empty or 'Close' not in data:
raise ValueError("No data downloaded.")
valid_symbols = []
for symbol in symbols:
if symbol in data['Close'].columns and not data['Close'][symbol].isna().all():
valid_symbols.append(symbol)
portfolio_returns = data['Close'][valid_symbols].pct_change().dropna() # Daily returns (dates x stocks)这将过滤掉所有从 yfinance 返回无效数据的股票代码。或者,您也可以创建一个失败股票代码列表,并将它们打印到控制台,以便更好地了解失败情况。
3、拟合 PCA 模型
sklearn 让 PCA 变得简单。对收益率进行拟合,以找到解释方差最大的主成分。
pca = PCA(n_components=5) # Top 5 components for deeper insight
pca.fit(portfolio_returns)
pct = pca.explained_variance_ratio_ # % variance per component
pca_components = pca.components_ # Loadings (components x stocks)n_components=5 选取解释方差最大的前五个主成分。拟合后,提取解释的方差和主成分。
在我的运行中,第一个主成分解释了约 29% 的方差;前五个主成分累计解释了约 44% 的方差。您的结果可能略有不同。
4、可视化主成分
可视化是阐明 PCA 数学原理的最佳方式。
cum_pct = np.cumsum(pct)
x = np.arange(1, len(pct) + 1, 1)
plt.subplot(1, 2, 1)
plt.bar(x, pct * 100, align="center")
plt.title('Contribution (%)')
plt.xlabel('Component')
plt.xticks(x)
plt.xlim([0, 6])
plt.ylim([0, 100])
plt.subplot(1, 2, 2)
plt.plot(x, cum_pct * 100, 'ro-')
plt.title('Cumulative contribution (%)')
plt.xlabel('Component')
plt.xticks(x)
plt.xlim([0, 6])
plt.ylim([0, 100])
plt.tight_layout() # Nicer spacing
plt.show()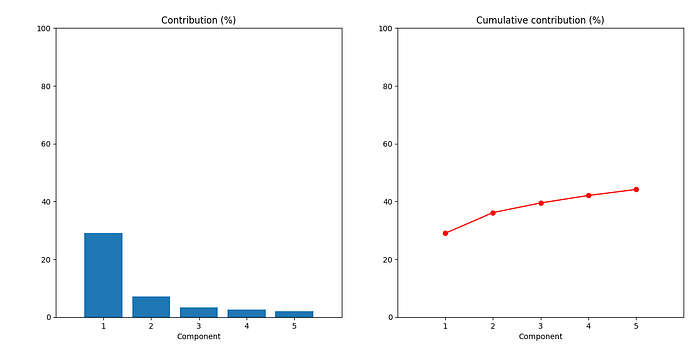
左侧条形图显示了每个组成部分的单独贡献:第一个组成部分解释了约 29%。右侧曲线显示的是累计贡献。在本例中,前五大因素贡献了约 44% 的总回报波动。
为了更好地理解这些因素,请尝试运行不同时间段的代码。如果我们更新时间段:
data = yf.download(symbols, start="2020-01-01", end="2021-12-31")
现在,第一个主成分的贡献突然变为约 25%,而前五大因素的累计贡献跃升至约 52%。您认为如果我们从 2020 年到 2024 年底进行测试会发生什么?
5、分离阿尔法因子
股价受一些未知因素的影响:市场贝塔系数、利率、疫情等等。主成分分析 (PCA) 可以将这些潜在因素识别为主成分。因子 1 通常是市场因素;其他因子则是潜在的阿尔法因素(例如,行业或宏观信号)。
计算每日因子收益率:
X = np.asarray(portfolio_returns)
factor_returns = X.dot(pca_components.T) # (dates x 5 factors)
factor_returns = pd.DataFrame(
columns=["f1", "f2", "f3", "f4", "f5"],
index=portfolio_returns.index,
data=factor_returns
)
factor_returns.head()每一行:当日投资组合收益中每个因子的占比。相似的股票具有相似的因子敞口——这是策略的关键。
6、可视化股票风险敞口
在三维空间中查看股票按因子聚类(风险敞口/载荷):
# Get loadings per stock (stocks x components)
loadings = pca.components_[:3].T # First 3 factors (n_stocks x 3)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# Plot stock positions, colored by f3 exposure
sc = ax.scatter(loadings[:, 0], loadings[:, 1], loadings[:, 2],
c=loadings[:, 2], cmap='viridis', s=20, alpha=0.6)
ax.set_xlabel('Factor 1 (Market Beta)')
ax.set_ylabel('Factor 2 (e.g., Growth)')
ax.set_zlabel('Factor 3 (e.g., Value)')
plt.colorbar(sc, ax=ax, label='Factor 3 Exposure')
plt.title('S&P 500 Stocks Clustered by Top 3 Factors')
plt.show()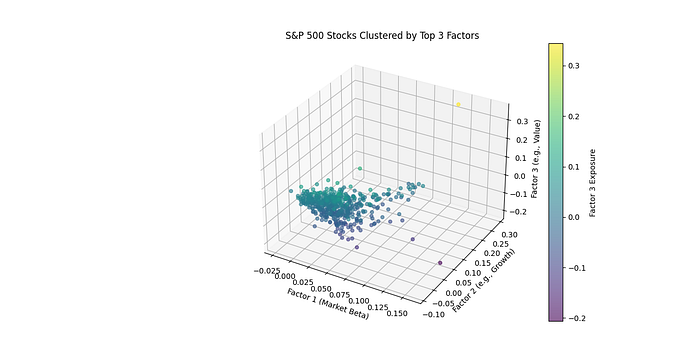
出现了不同的聚类:科技股在一个区域(增长倾向),能源股在另一个区域(价值/周期性)。对于 2020-2025 年(新冠疫情时代),因子 1 可能反映了“不确定性”,黄金股因对冲风险而上涨,科技股则因经济担忧而暴跌。
7、RAPIDS 的强大功能
上述实现并未充分发挥 RAPIDS 的强大功能。对于拥有数百万行或数千个特征的大型数据集,cuML 可以将运行时间从数小时缩短到数秒或数分钟。对于当前标普500指数股票约5年(2020年1月1日至2025年10月15日,约1429天,已计入交易日)的数据集,生成的投资组合收益矩阵的形状为(1429, 503)(行数×列数)。以下是一些能够充分发挥其优势的具体应用场景:
- 利用大规模协方差矩阵计算进行投资组合优化。投资组合经理使用现代投资组合理论(MPT)通过计算股票收益的协方差矩阵来优化资产配置,从而在给定收益下最小化风险。对于10000只全球股票,如果拥有10年的每日收益数据,则数据量约为2500万个。NVIDIA A100 GPU可以在5-10秒内完成此计算。
- 利用聚类进行市场机制检测的高频交易。公司通过对日内价格走势进行聚类分析来识别市场机制(例如,牛市、熊市或波动性),并调整交易策略。对 1000 只股票一个月内的 1 分钟收益率进行聚类分析,可生成约 4000 万个数据点。
利用 PCA 对大型 ETF 数据集进行风险因子建模。风险分析师应用 PCA 对数千只 ETF(例如,5000 只 ETF)五年(约 1260 个交易日)的收益率进行分解,以识别潜在的风险因子(例如,市场因子、行业因子或波动性因子)。这将生成一个形状为 (1260, 5000) 的矩阵,包含约 630 万个数据点。
- 在所有这些情况下,利用 GPU 进行并行矩阵计算可以大幅缩短计算时间。剩下的唯一问题就是数据的可用性。
8、结束语
您已经掌握了基础知识:拟合 PCA 模型、识别因子、可视化风险敞口。现在开始实验吧!
原文链接:Quant Finance: Alpha Discovery is 50x Faster on GPU with RAPIDS
汇智网翻译整理,转载请标明出处
