LLM基础:矩阵和向量
今天,我们将讨论矩阵乘法,以及这些数值计算如何在帮助AI模型“思考”中起到巨大作用。

如果你想真正了解机器学习,就不要寻找其他方法了。
随着人工智能变得越来越强大,人们自然会担心它会“取代你的工作”。
根据我的看法,如果你有学习的能力和不断探索新事物的好奇心,没有什么能阻止你。
这是关于机器学习数学的三篇系列文章中的第二篇。
今天,我们将讨论矩阵乘法,以及这些数值计算如何在帮助AI模型“思考”中起到巨大作用。
1、矩阵乘法到底是什么?
我认为矩阵乘法是依次对一个向量应用两个变换。
假设我们首先将一个向量旋转90度,然后向右倾斜。
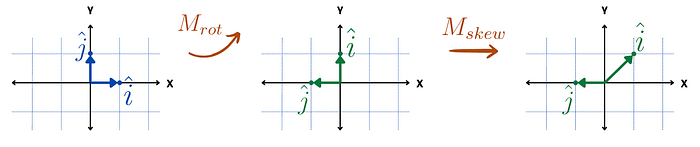
这在数学上会是什么样子呢?
操作将是:
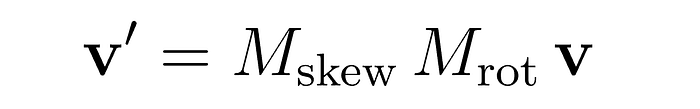
这意味着先应用Mrot,然后对结果应用Mskew。
但问题是:我们可以用一个单独的矩阵来表示这个完整的变换吗?
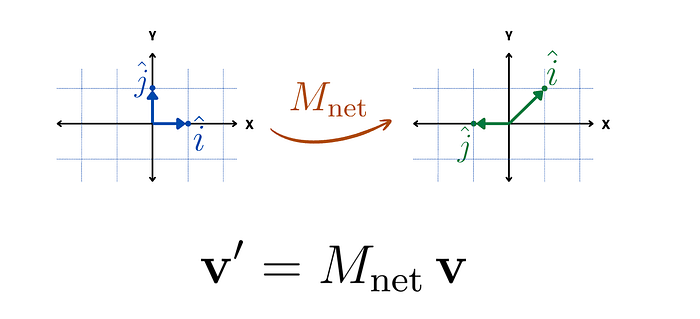
结果是,我们只需“相乘”Mskew和Mrot即可。
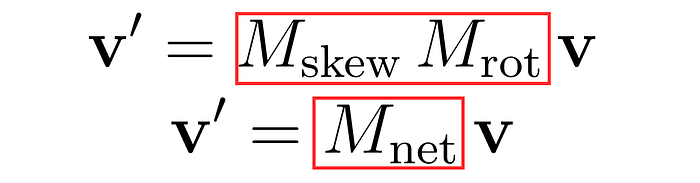
如何计算Mnet?就像我们在之前的博客中看到的一样,我们可以找到î和ĵ的最终位置,并将它们作为Mnet的列。
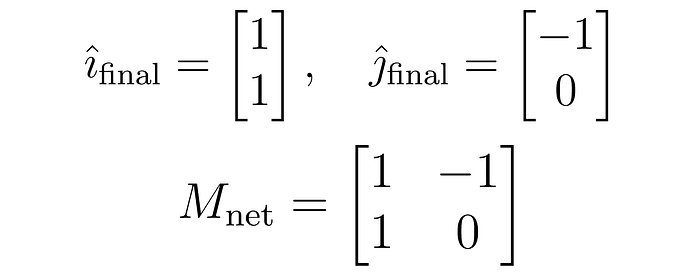
但这是否真的等同于单独的变换矩阵相乘呢?
是的,原因如下:
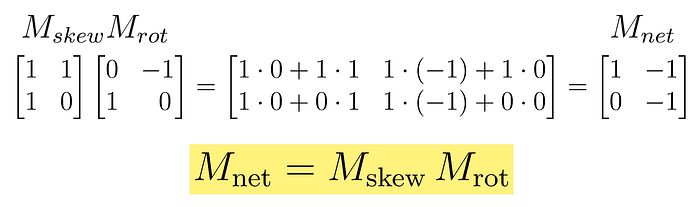
有趣的是:
另一个线性变换的线性变换可以归结为一个等效的线性变换。
这就是为什么神经网络层之间有激活函数的原因。(稍后我们会看到这一点)
2、矩阵乘法中的最终维度是什么?
如果你在乘两个矩阵或者一个矩阵和一个向量时,最重要的是要理解输入和输出的维度。
关键规则很简单:内部维度必须匹配,结果取外部维度。
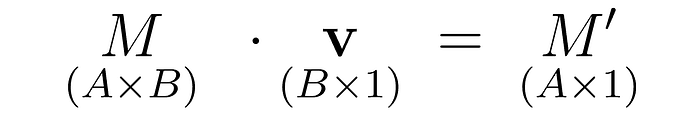
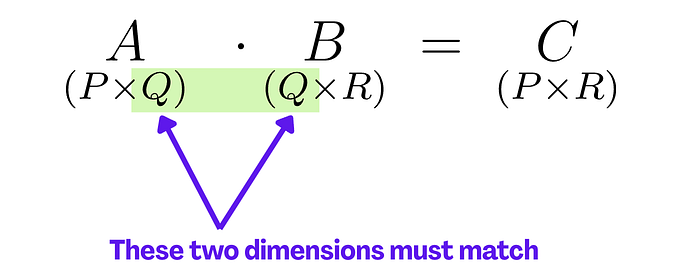
这是一个数值示例:
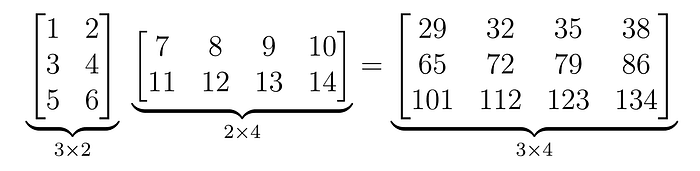
3、这个想法在现实世界的人工智能中有多重要?
每个Transformer层都有一个MLP,其基本结构就是这些矩阵乘法。
让我解释一下。
每个标记都会被转换成一个向量,然后“通过LLM的各层传递”。
在每一层中,该向量经过一系列操作,如图所示:
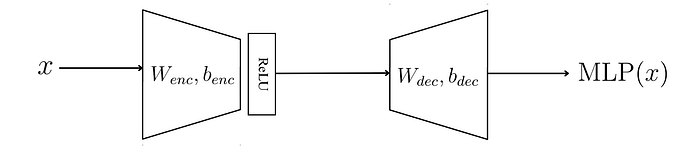
如果这令人困惑,不用担心,我会逐步解释。
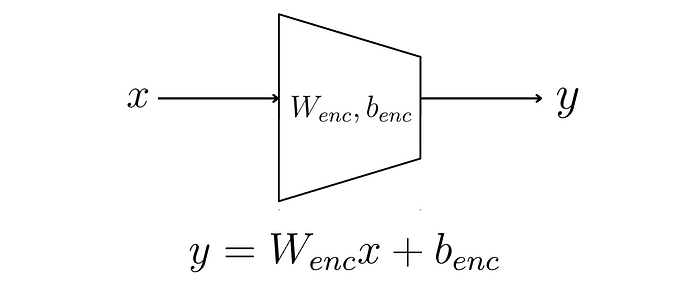
梯形代表“线性投影”矩阵。
“投影”只是一个线性变换,只是输出向量与输入向量的维度不同。

接下来,我们通过ReLU(一种“激活函数”)。
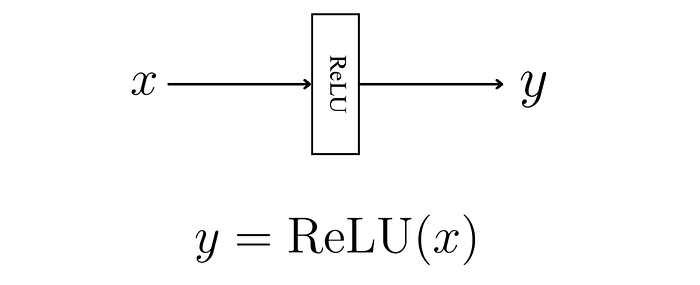
这会将小于零的输入值设为零,其他值保持不变。
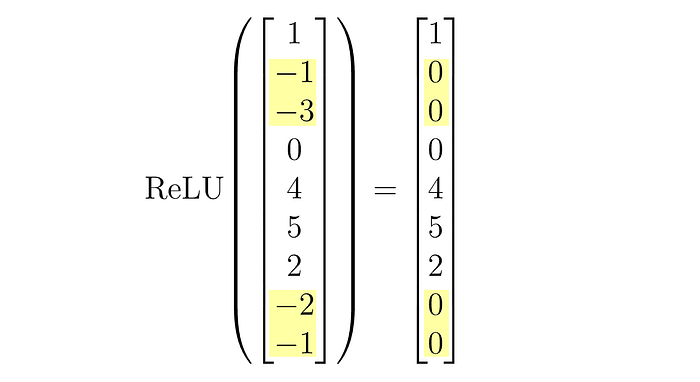
最后,我们通过最终的投影将其返回到原始向量空间。
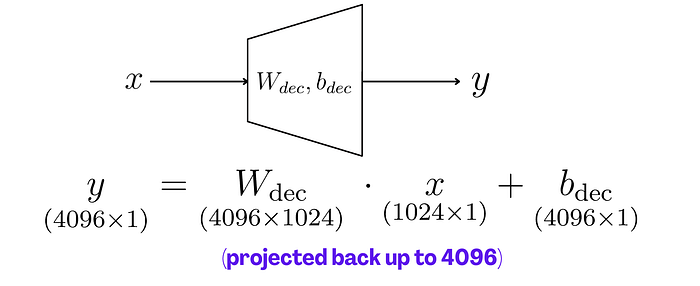
4、为什么我们需要ReLU函数?
我们使用ReLU是因为它是一个非线性函数,并为MLP层添加了非线性。
想象一下完全没有ReLU函数。
我们将x向下投影然后再向上投影。
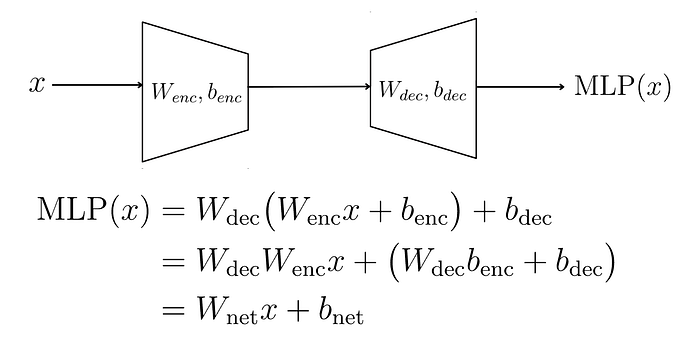
两个矩阵串联等价于一个单一的线性变换。矩阵是冗余的——这不是我们想要的。
5、给你的挑战
你正在处理一个Transformer模型,其中每个标记都表示为一个512维的向量。
在MLP层中,你希望:
- 向下投影 (W₁):将512维的标记向量转换为128维的“压缩”表示。
- 应用ReLU:保持非线性。
- 向上投影 (W₂):将128维的向量转换回原始的512维空间。
W₁和W₂这两个投影矩阵的维度应该是多少?
附加问题
如果你同时处理32个标记(因此你的输入是一个32×512的矩阵,每行是一个标记),那么W₁、W₂和压缩表示的维度是多少?写出矩阵运算。
在评论中告诉我你的答案!
6、结束语
在这篇博客中,我们讨论了矩阵乘法如何作为顺序变换起作用,以及如何考虑这些操作中的维度。
我们还看了Transformer中的MLP作为一个实际例子,说明矩阵运算构成了现代AI模型的基础。
有趣的是:神经网络中的每一个“层”本质上都是关于矩阵乘法。
在本系列的最后一篇博客中,我们将讨论特征向量、特征值,如何在任何矩阵变换中计算它们,以及这些概念如何与更具体的主题如主成分分析联系起来。
原文链接:LLMs think in matrices and vectors.
汇智网翻译整理,转载请标明出处
