从第一性原理出发的LLM强化学习
为了建立对语言模型强化学习的坚实理解,我们将采取逐步的方法。我们将从本概述中的基本概念和定义开始,然后探讨用于使用人类反馈进行强化学习微调语言模型的常用算法。

大型语言模型(LLMs)在各种任务中表现出令人印象深刻的能力。这种成功的一个关键部分是使用了强化学习,特别是称为从人类反馈中进行强化学习(RLHF)的方法。尽管RLHF在塑造LLMs的最终性能方面起着重要作用,但大多数开源社区的工作更侧重于监督学习方法,如监督微调(SFT)。
有几点原因导致强化学习受到的关注较少。
- 一个主要原因是RLHF需要特殊的数据,即人类反馈或偏好数据,这更难收集和整理。
- 另一个原因是许多实践者更熟悉监督学习,对强化学习方法不太熟悉。这种知识差距使得在实际设置中采用RL更加困难。我自己也包括在内。
因此,目标是通过从零开始建立对强化学习的实用理解来消除这种知识差距。
为了建立对语言模型强化学习的坚实理解,我们将采取逐步的方法。
- 我们将从本概述中的基本概念和定义开始。
- 我们将探讨用于使用人类反馈进行强化学习微调语言模型的常用算法。
在本文的最后,我们会看到这些想法在实践中很容易使用。
现在让我们看看强化学习在LLM上下文中的含义。
注意:在本文中,我将使用“agent/s”这个术语来指代我们想要微调的LLMs。
1、什么是强化学习?
从高层次来看,强化学习(RL)是训练机器学习模型的另一种方法。我们有几种方法可以微调神经网络。其中最常见的是监督学习和自监督学习,用于语言模型。
监督学习
在监督学习中,数据集包含输入序列及其对应的标签。目标是训练模型从输入中预测正确的标签。
例如,要微调像BERT这样的语言模型来分类句子是否包含明确语言,我们可以使用标记为明确或不明确的句子数据集。训练过程包括以下步骤:
- 从数据集中采样一个小批量
- 使用模型预测标签
- 计算损失(例如,交叉熵)
- 反向传播梯度
- 更新模型权重
自监督学习
自监督学习遵循类似的过程,但不需要外部标签。相反,监督来自数据本身的结构。
例如,语言模型通常通过预测序列中的下一个词来预训练,使用前面的词作为输入。由于下一个词已经存在于数据中,不需要手动标记。
2、什么时候强化学习有用?
当我们要模型从反馈中学习而不是固定标签时,强化学习是有用的。与依赖已知正确输出的监督学习不同,RL通过试错来训练模型。模型生成一个输出,接收以奖励形式的反馈,并根据该奖励更新自身。
在语言模型的背景下,这应用于从人类反馈中进行强化学习(RLHF)。模型生成文本响应,人类根据其质量给出评分。然后模型使用这个评分来调整其行为,并随着时间的推移学习生成更高品质的输出。

在从人类反馈中进行强化学习(RLHF)时,我们不能使用标准的监督学习直接训练模型以遵循人类偏好。这是因为人类给出的分数无法轻松表示为数学函数。这是一种主观评价,我们无法计算通过人类判断的梯度。
监督学习依赖于有一个明确定义的损失函数,我们可以对其进行微分并通过模型反向传播。但在RLHF中,人类反馈是一个黑箱,我们得到一个分数,但我们不知道这个分数是如何确定的,也无法直接将其与模型的输出连接起来。
注意:在传统的RL环境中,挑战在于环境是一个不可微分的黑箱。我们收到一个奖励,但没有直接的方法通过监督学习来训练网络,因为奖励信号无法反向传播。
对于LLMs,有一个重要的区别。奖励通常由奖励模型提供,这是可微分的。这使得环境实际上变得可微分,并允许我们使用监督学习(例如DPO微调基于这种方法)端到端地训练模型。然而,如果分数是直接由人类提供的,并且没有奖励模型(或额外的可训练层)来自动化反馈,那么反向传播是不可能的。
3、为什么强化学习有效
强化学习在这种情况下有效,因为它允许我们从不可微分的反馈中学习。我们可以基于任何类型的分数或信号来训练语言模型,即使它来自人类、基于规则的系统或其他模型。奖励可以反映我们想要的任何价值观或目标,比如让模型更有帮助、更安全、更诚实或能够使用工具。
4、强化学习的结构
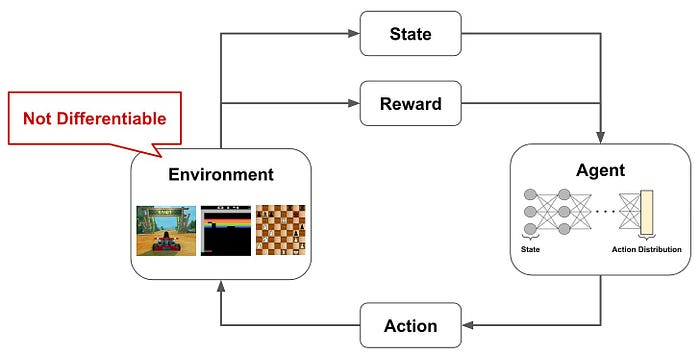
强化学习问题通常遵循一个常见的结构。代理与环境互动,根据当前状态采取行动,并根据这些行动的结果获得奖励。
代理的行动可以改变环境的状态,目标是学习一种最大化总奖励的策略。然而,奖励并不总是在每次行动后给予。在许多情况下,奖励是延迟的,并取决于一系列行动。这被称为长奖励范围,只有持续、正确的决策才能带来积极的结果。
5、马尔可夫决策过程(MDP)
为了更正式地描述强化学习,我们可以使用马尔可夫决策过程(MDP)来表述系统。MDP为建模代理和环境之间的交互提供了清晰的结构。它包括以下元素:

MDP组件
- 状态:代理可能处于的不同情况。
- 动作:代理从每个状态可以做出的选择。
- 奖励:采取行动后收到的反馈。
- 转移:决定行动后状态如何变化的规则。
- 策略:代理的策略,将状态映射到可能动作的概率分布。
在马尔可夫决策过程中,状态和动作通常表示为离散值,而奖励是实数。有两个关键函数定义代理在环境中的操作方式:
- 策略函数:以当前状态作为输入,返回可用动作的概率分布。这指导代理选择动作。
- 转移函数:给定当前状态和选定的动作,此函数确定环境的下一个状态。
有了这些函数,代理逐步与环境互动。在每一步,策略根据当前状态选择一个动作,环境转移到一个新的状态,并可能给予奖励。这个过程随着时间的推移继续,代理从其动作的结果中学习。
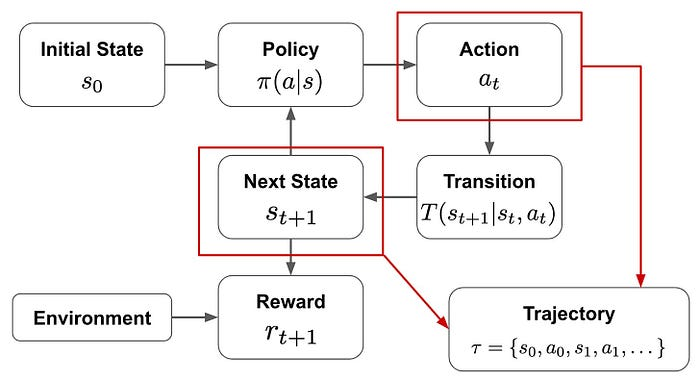
6、代理 vs 策略和回报
一个常见的问题是代理与策略有何不同。代理是存在于环境中的实体,而策略是代理用来决定其动作的策略。策略将每个状态映射到可能动作的概率分布,代理使用它来做决定。我们的目标是学习一个策略,使代理随着时间的推移获得最高的可能奖励。
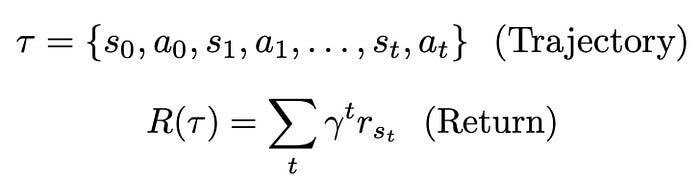
随着代理在环境中移动,它创建了一个称为轨迹的状态和动作序列。每个动作可能会导致一个奖励,总回报是轨迹中收集的所有奖励的总和。然而,未来的奖励会使用一个称为γ(伽马)的因子进行折扣。这个折扣因子确保即时奖励比遥远的未来奖励更重要。
强化学习的主要目标是训练代理以最大化其轨迹的总回报。这是通过找到一个在遵循时产生最高可能预期回报的策略来实现的。

在实践中,这意味着我们旨在学习一个随着时间推移产生更好动作序列的策略。这些动作应导致产生更高奖励的状态,即使奖励是在几步之后。
7、示例应用
为了使RL设置更具体,考虑一个简单的环境,其中代理必须在一个2 × 3网格中导航。目标是从起始位置移动到特定的目标位置。代理到达目标时获得+10的奖励,踩入红色方块时获得-10的奖励。
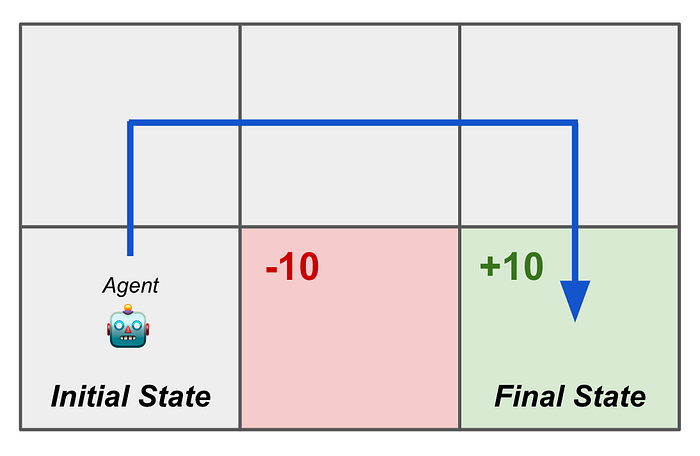
环境本身是网格。代理的状态是它的当前位置,可以用一个one-hot编码向量表示。策略使用一个前馈神经网络实现,该网络以这个one-hot向量作为输入,并输出四个可能动作(向上、向下、向左或向右)的概率分布。
转换函数根据所选动作更新代理的位置,同时防止任何超出边界的操作。代理必须学会在不踩入红色方块的情况下到达目标。
这个例子反映了强化学习问题中的常见特征:环境不是可微分的,奖励是延迟的。代理必须学会采取一系列正确的动作以达到目标并最大化其总回报。
8、将强化学习应用于语言模型
网格导航示例代表了强化学习的经典应用,其中代理学习与外部环境互动。类似的RL方法已用于Atari游戏、围棋等棋盘游戏和自动驾驶等领域。
我们将同样的原则应用于微调语言模型。虽然任务非常不同,但强化学习的核心组件,代理、策略、环境、动作和奖励,可以映射到语言建模设置中。
语言模型被训练执行下一个token预测。给定一个输入序列,模型预测最可能的下一个token。在文本生成过程中,这个过程以自回归的方式重复:
- 预测下一个token
- 将预测的token添加到输入中
- 使用更新后的序列重复该过程
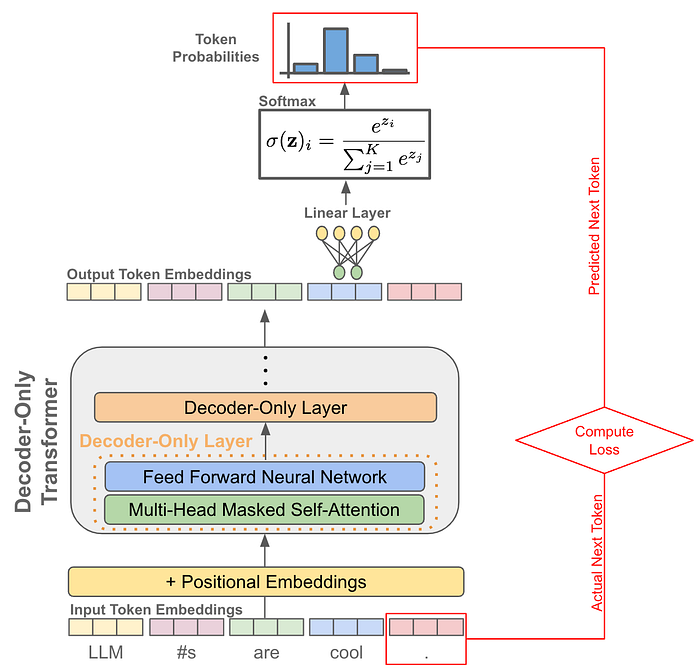
从强化学习的角度来看,我们可以使用熟悉的RL组件来描述这个过程:
- 语言模型(代理)充当策略
- 它的状态可能是当前提示或上下文
- 动作是它生成的下一个token
- 环境是文本生成过程
- 奖励来自对生成输出的反馈,这来自人类或基于人类偏好的奖励模型。
尽管这种设置不同于传统的RL环境如网格导航,但它遵循相同的结构。
9、重要术语和定义
现在,我们已经建立了强化学习的核心结构,了解一些在该研究领域中经常出现的重要术语是有帮助的:
轨迹:轨迹是一系列状态和动作,表示代理在环境中采取的步骤。
回合:回合指的是代理从起始状态到终止状态的完整运行。例如,在2 × 3网格中到达目标形成一个回合。
回报:回报是轨迹中收集的总奖励。由于早期获得的奖励通常比后期获得的奖励更有价值,回报是通过折扣因子计算的。

折扣因子 (γ):折扣因子是指确定未来奖励当前价值的基本思想。如上图所示,我们在RL中通过指数折扣因子处理折扣。较低的折扣因子对未来的奖励价值较低,鼓励短期收益,而较高的折扣因子则强调长期成功。
在线策略 vs 离线策略:在RL中,目标策略是我们想要改进的策略。行为策略是当前用于生成动作的策略。当两者相同时,方法是在线策略。如果它们不同,则是离线策略。
ε-贪婪策略:这种策略平衡学习和决策。以概率 1 − ε,代理选择具有最高估计回报的动作。以概率 ε,它选择一个随机动作以探索新可能性。
10、Q-Learning:一个简单的RL算法
让我们看一下我们的第一个RL算法。这个算法叫做Q-Learning,它被广泛使用。它将为我们提供一个很好的介绍,了解RL算法是如何工作的。在理解Q-Learning之后,我们将探讨其深度学习扩展,深度Q-Learning,它用于训练深度神经网络。
10.1 什么是Q-Learning?
Q-Learning是一种无模型的强化学习算法。这意味着我们不需要学习环境的转移或奖励函数。相反,我们依靠与环境的交互来更新我们对每个状态下哪些动作有价值的理解。
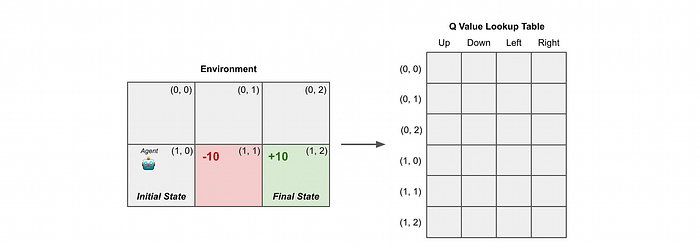
核心思想是学习一个Q函数,它估计在给定状态采取特定动作并遵循某种策略后的预期回报。Q函数帮助代理决定从当前状态出发,哪个动作很可能导致最高的长期回报。
Q值存储在一个查找表中,表中的每个单元格保存Q值,它估计在特定状态下采取特定动作的预期回报。
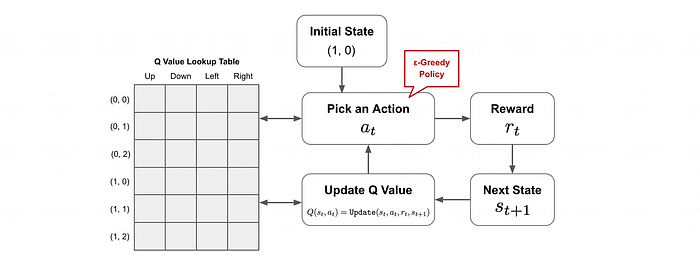
一开始,所有的Q值都被初始化为零。随着代理探索环境,它使用贝尔曼方程更新这些值,该方程根据观察到的奖励和估计的未来回报调整估计。
随着时间的推移,代理根据收到的奖励更新这个表,并利用它做出更好的决策。
10.2 Q-Learning算法
Q-learning算法从将所有Q值初始化为零并选择一个起始状态开始。代理然后重复以下步骤:
- 使用ε-greedy策略从当前状态中选择一个动作。
- 执行该动作并从环境中接收奖励和下一个状态。
- 使用贝尔曼方程更新当前状态-动作对的Q值。
贝尔曼更新考虑即时奖励、当前Q值和下一个状态的最佳可能未来回报。由于下一个状态可能有多个可能的动作,Q-learning在计算更新时使用这些动作中的最大Q值。
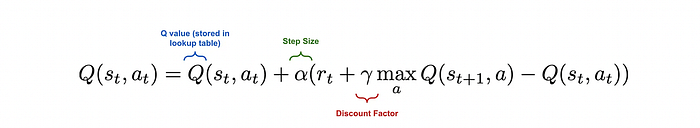
这种方法逐渐改进Q表,直到它反映出每个状态的最佳可能决策。
Q-learning使用ε-greedy策略在训练期间选择动作。这意味着代理通过偶尔选择随机动作进行探索,确保它访问广泛的州。
然而,在更新Q值时,算法假设一个贪婪策略,无论实际将采取哪个动作,都使用下一个状态的最大Q值。这种行为策略(用于行动)和目标策略(用于更新)之间的分离使Q-learning成为一个离线策略算法。
注:Q-learning已被证明在足够更新和适当探索的情况下收敛到任何有限马尔可夫决策过程的最优策略。这意味着,随着时间的推移,它将学习最大化回报的最佳可能策略。
简单Q-Learning算法的代码实现,用于直观理解:
#定义环境
import numpy as np
n_states = 16
n_actions = 4
goal_state = 15
Q_table = np.zeros((n_states, n_actions))
#设置超参数
learning_rate = 0.8
discount_factor = 0.95
exploration_prob = 0.2
epochs = 1000
#实现Q-Learning算法
for epoch in range(epochs):
current_state = np.random.randint(0, n_states)
while current_state != goal_state:
if np.random.rand() < exploration_prob:
action = np.random.randint(0, n_actions)
else:
action = np.argmax(Q_table[current_state])
next_state = (current_state + 1) % n_states
reward = 1 if next_state == goal_state else 0
Q_table[current_state, action] += learning_rate * \
(reward + discount_factor *
np.max(Q_table[next_state]) - Q_table[current_state, action])
current_state = next_state
print(Q_table)
#检查更新后的Q_table。
#学习的Q表显示每个状态-动作对的预期奖励,
#靠近目标状态(状态15)的Q值较高,
#表明导致达到目标的最佳动作。
10.3 深度Q-Learning
深度Q-Learning(DQL)直接建立在基本Q-Learning算法的原则上。主要区别在于,而不是使用查找表来存储Q值,我们使用深度神经网络来近似Q函数。这使得算法能够处理更大和更复杂的状态空间,在这种情况下,表格方法是不切实际的。它使代理能够直接从高维输入(如图像或序列)中学习,并在相似状态之间泛化。
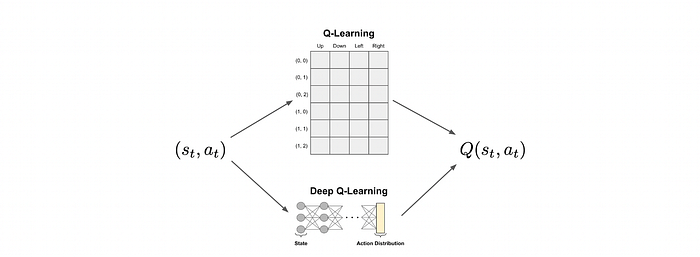
Q-learning的主要限制之一是查找表的大小,它随着可能状态和动作的数量而增长。在复杂环境中,如带有视觉输入的视频游戏或现实世界任务,状态-动作对的数量可能非常大。存储和更新每个对的Q值变得不可能且难以追踪。
深度Q-Learning通过使用神经网络来近似Q函数来解决这个问题。而不是为每个状态-动作对存储一个值,我们训练一个网络,该网络以当前状态作为输入,并输出所有可能动作的Q值。模型只需存储神经网络的参数,这些参数可以在收集新经验时进行更新。这使得该方法更具可扩展性。
10.4 深度Q-Learning算法
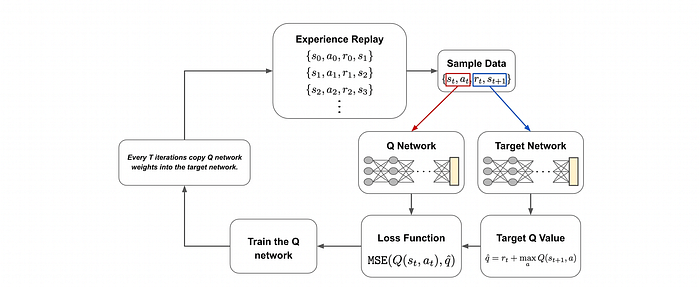
深度Q-Learning使用两个神经网络:Q网络和目标网络。这两个网络具有相同的架构,但在训练期间扮演不同的角色。网络的结构可以根据特定问题而变化。
开始训练时,代理通过使用当前Q网络和ε-greedy策略与环境互动来收集数据。这个收集和存储经验的过程称为经验回放。交互、状态、动作、奖励和下一个状态存储在缓冲区中。

在训练期间,从该缓冲区中抽取数据批次。Q网络接收当前状态并预测所采取动作的Q值(预测的Q值)。同时,目标网络接收下一个状态并估计最佳下一个动作的Q值(目标Q值)。
一旦我们有了预测的Q值、目标Q值和观察到的奖励,我们就可以用它们来更新Q网络。训练目标是将预测的Q值与目标Q值之间的均方误差(MSE)最小化。在此过程中,目标网络保持不变。
每隔几个训练步骤,我们通过将Q网络的权重复制到目标网络来更新目标网络。这种渐进式的更新有助于稳定学习,防止目标Q值在训练模型时变化过快。
经验回放缓冲区在训练过程中继续增长,保留所有过去的观察结果。这使模型能够从广泛的历史经验中学习。
11、为什么要使用目标网络?
在Q-learning中,我们总是使用两个Q值来计算更新:
- 一个是当前状态-动作对的Q值,
- 一个是下一个状态的最佳动作的Q值。
在深度Q-Learning中,我们可以使用同一个神经网络来计算这两个值。然而,由于Q网络在每次批处理后都会更新,使用它来计算两个估计会导致不稳定的目标,这些目标不断变化。
为了解决这个问题,深度Q-Learning引入了目标网络。它通过在几个训练步骤中保持不变来提供一个稳定的参考。这减少了目标值的波动,从而实现了更可靠的学。
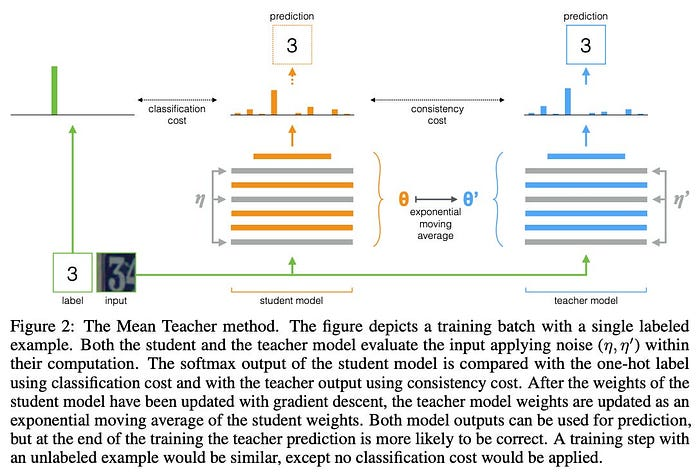
使用单独的网络来生成训练目标,称为知识蒸馏,是深度学习中常见的想法。它允许一个模型(教师)指导另一个模型(学生)的训练,通常有助于学生学习更稳定或可泛化的表示。
在深度Q-Learning中,目标网络扮演教师的角色,而Q网络是学生。为了保持稳定性,一些方法走得更远,例如平均教师方法将教师的权重更新为学生的权重的指数移动平均。这提供了更平滑的更新,并有助于避免训练期间目标值的突然变化。
DQL的基本实现供参考:
class DQNAgent:
def __init__(self, state_size, action_size):
self.n_actions = action_size
# we define some parameters and hyperparameters:
# "lr" : learning rate
# "gamma": discounted factor
# "exploration_proba_decay": decay of the exploration probability
# "batch_size": size of experiences we sample to train the DNN
self.lr = 0.001
self.gamma = 0.99
self.exploration_proba = 1.0
self.exploration_proba_decay = 0.005
self.batch_size = 32
# We define our memory buffer where we will store our experiences
# We stores only the 2000 last time steps
self.memory_buffer= list()
self.max_memory_buffer = 2000
# We creaate our model having to hidden layers of 24 units (neurones)
# The first layer has the same size as a state size
# The last layer has the size of actions space
self.model = Sequential([
Dense(units=24,input_dim=state_size, activation = 'relu'),
Dense(units=24,activation = 'relu'),
Dense(units=action_size, activation = 'linear')
])
self.model.compile(loss="mse",
optimizer = Adam(lr=self.lr))
# The agent computes the action to perform given a state
def compute_action(self, current_state):
# We sample a variable uniformly over [0,1]
# if the variable is less than the exploration probability
# we choose an action randomly
# else
# we forward the state through the DNN and choose the action
# with the highest Q-value.
if np.random.uniform(0,1) < self.exploration_proba:
return np.random.choice(range(self.n_actions))
q_values = self.model.predict(current_state)[0]
return np.argmax(q_values)
# when an episode is finished, we update the exploration probability using
# espilon greedy algorithm
def update_exploration_probability(self):
self.exploration_proba = self.exploration_proba * np.exp(-self.exploration_proba_decay)
print(self.exploration_proba)
# At each time step, we store the corresponding experience
def store_episode(self,current_state, action, reward, next_state, done):
#We use a dictionnary to store them
self.memory_buffer.append({
"current_state":current_state,
"action":action,
"reward":reward,
"next_state":next_state,
"done" :done
})
# If the size of memory buffer exceeds its maximum, we remove the oldest experience
if len(self.memory_buffer) > self.max_memory_buffer:
self.memory_buffer.pop(0)
# At the end of each episode, we train our model
def train(self):
# We shuffle the memory buffer and select a batch size of experiences
np.random.shuffle(self.memory_buffer)
batch_sample = self.memory_buffer[0:self.batch_size]
# We iterate over the selected experiences
for experience in batch_sample:
# We compute the Q-values of S_t
q_current_state = self.model.predict(experience["current_state"])
# We compute the Q-target using Bellman optimality equation
q_target = experience["reward"]
if not experience["done"]:
q_target = q_target + self.gamma*np.max(self.model.predict(experience["next_state"])[0])
q_current_state[0][experience["action"]] = q_target
# train the model
self.model.fit(experience["current_state"], q_current_state, verbose=0)
12、结束语
DQNs非常高效,但仍有一些改进的空间。在计算Q-target值时,我们使用正在更新的相同神经网络。因此,更新网络权重后,Q值会向Q-target移动,但Q-target也会朝同一方向移动。这导致优化不稳定,就像追逐自己的目标一样。此外,从记忆缓冲区中随机选择经验可能不是最优的。代理可以从专注于TD误差较大的经验中受益更多。
为了解决这两个问题,我们可以使用双重Q网络和优先经验回放。我将在以后的文章中探讨这些内容。
原文链接:Reinforcement Learning for LLMs from First Principle
汇智网翻译整理,转载请标明出处
